Moto circolare uniforme – 9

9

Su due ruote in moto circolare uniforme

Due ruote sono in contatto come mostrato in figura. Entrambe si muovono di moto circolare uniforme e la loro velocità tangenziale v è identica. Se il rapporto tra le frequenze è pari a 2,2

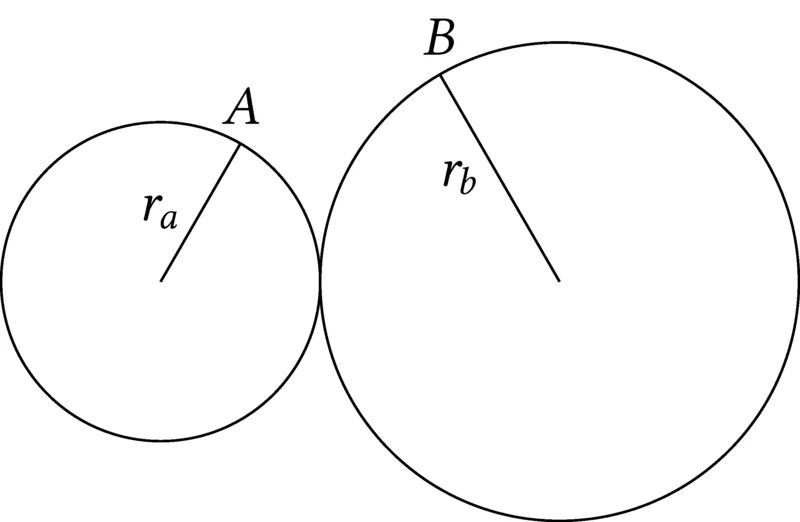
  • Calcola il rapporto tra i periodi
  • Calcola il rapporto tra le accelerazioni centripete

Soluzione

Prima di tutta ricordiamo che il periodo T è definito come:

    \[T = \frac{1}{f}\]

dove f è la frequenza di rotazione. Dal momento che la frequenza di rotazione della ruota più piccola B sarà ovviamente maggiore di quella A sappiamo che:

    \[\frac{f_B}{f_A} = 2,2\]

Quindi,

    \[\frac{T_B}{T_A} = \frac{1/f_B}{1/f_A} = \frac{f_A}{f_B} = \frac{1}{2,2} = 0,45\]

Per il rapporto tra le accelerazioni centripete ricordiamoci che l’accelerazione centripeta è definita come:

    \[a = \frac{v^2}{r}\]

dove r è la distanza rispetto al centro di rotazione. Nel nostro caso sappiamo che la velocità tangenziale v è uguale per le due ruote ma non abbiamo nessuna informazione sui raggi r_A ed r_B.

Sfruttiamo la definizione di velocità tangenziale:

    \[v = \omega r\]

e la definizione di velocità angolare:

    \[\omega = 2\pi f\]

Combinando insieme le due definizioni otteniamo:

    \[\frac{v}{r} = 2\pi f\]

Dalla formula inversa otteniamo per la ruota A:

    \[r_A = \frac{v}{2\pi f_A}\]

mentre per la ruota B otteniamo:

    \[r_B = \frac{v}{2\pi f_B}\]

Facciamo il rapporto dei raggi:

    \[\frac{r_B}{r_A} = \frac{v/2\pi f_B}{v/2\pi f_A} = \frac{f_A}{f_B} \]

Il rapporto tra le accelerazioni centripete è definito come:

    \[\frac{a_B}{a_A} = \frac{v^2/r_B}{v^2/r_A} = \frac{r_A}{r_B} = \frac{f_B}{f_A} = 2,2\]